
We start by defining the finite difference operators for the x and y directions respectively. We then convolve the original image by the Dx operator and the Dy operator, creating two new images that detect the horizontal and vertical edges respectively. To calculate the gradient magnitude, I stacked the x and y partial derivative images and took the L2 norm to find the final pixel values.






I noticed some key differences from the DoG filter versus the finite difference operator. The edge lines seem to be much thicker, implying that there were a lot more "activations" of the DoG filter. You can clearly see the outline of the man and his camera. There is also less noise since our threshold did not have to be too low to capture the relevant edges.
I also noticed that doing the entire process in a single convolution by first blurring the finite difference operators with the Gaussian kernel resulted in the same exact image.





Based on visual observation, the resharpened image seems to be at the same level of "sharpness" as the original.


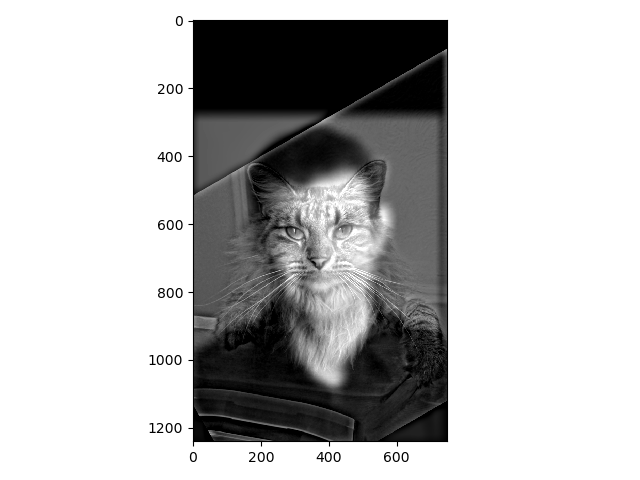



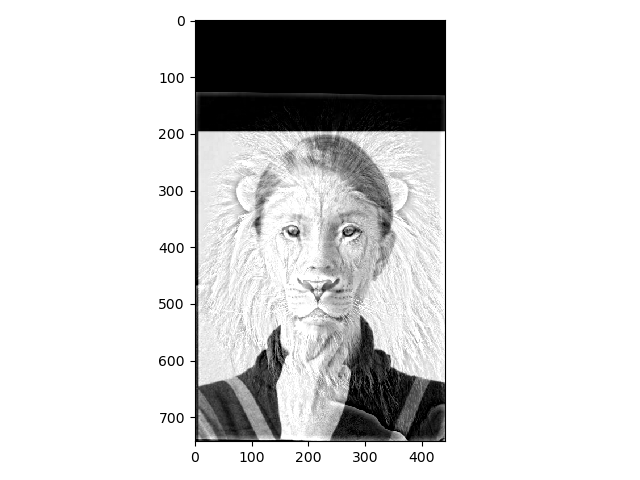


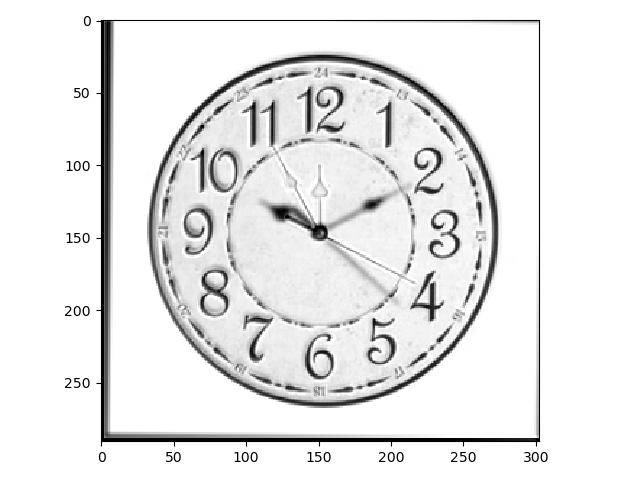
For these images the blend is a little subtle - you can see that we used a low-pass filter for the first clock (whose hands are blurred) and a high pass filter for the second clock (outlined hands)

























